Grouping Entries
The three dimensions of a namespace.Willow lets authors place Entries in namespaces, and within each namespace, Entries are arranged according to three orthogonal dimensions: subspace_id, path, and timestamp. This suggests a powerful way of thinking about Willow: a namespace is a collection of points (Entries) in a three-dimensional space. Or more accurately, a namespace is a mapping from points in this three-dimensional space to hashes and sizes of Payload.
This viewpoint enables us to meaningfully group Entries together. An application might want to access all chess games that a certain author played in the past week. This kind of query corresponds to a box (a rectangular cuboid to use precise terminology) in the three-dimensional Willow space.
In this document, we develop and define a vocabulary for grouping Entries based on their entry_subspace_id, entry_path, and entry_timestamp. These definitions are not necessary for defining and understanding the core data model, but we make heavy use of them in our recommended capability system and our invalid-reference.
Ranges
Ranges are simple, one-dimensional ways of grouping Entries, they can express groupings such as “last week’s Entries”. A range is either a closed range or an open range. A closed range consists of a start value and an end value , an open range consists only of a start value. A range includes all values greater than or equal to its start value and strictly less than its end value (if it is has one). A range is empty if it includes no values.
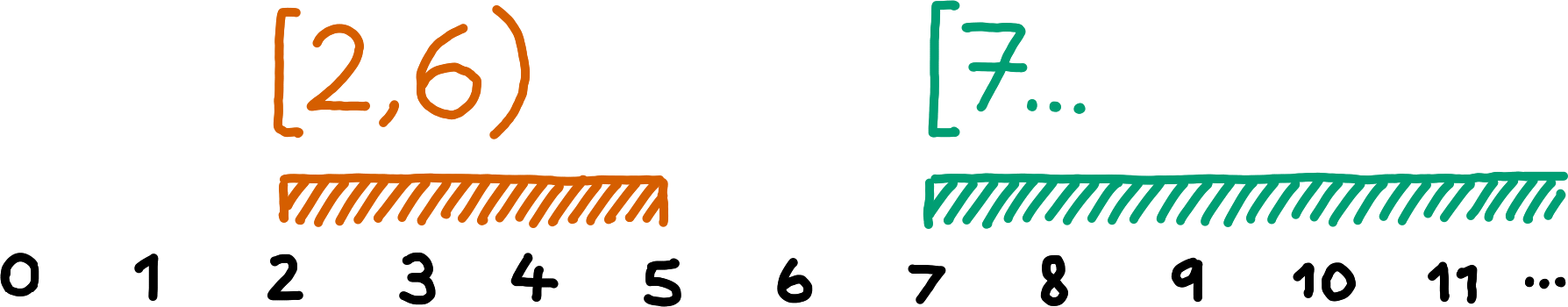
The Willow protocols use three types of ranges:
A range of SubspaceIds. A SubspaceId must be greater than or equal to this to be included in the range. The ordering must be given by a protocol parameter. If open, the range is an open range. Otherwise, a SubspaceId must be numerically strictly less than this to be included in the range. The ordering must be given by a protocol parameter.} If open, the range is an open range. Otherwise, a Path must be lexicographically strictly less than this to be included in the range.}A range of Timestamps. }Let r1 and r2 be ranges (over the same types of values). The intersection of r1 and r2 is the range whose start value is the greater of the start values of r1 and r2, and whose end value is the lesser of the end values of r1 and r2 (if both are closed ranges), the one end value among r1 and r2 (if exactly one of them is a closed range), or no end value (if both r1 and r2 are open ranges).
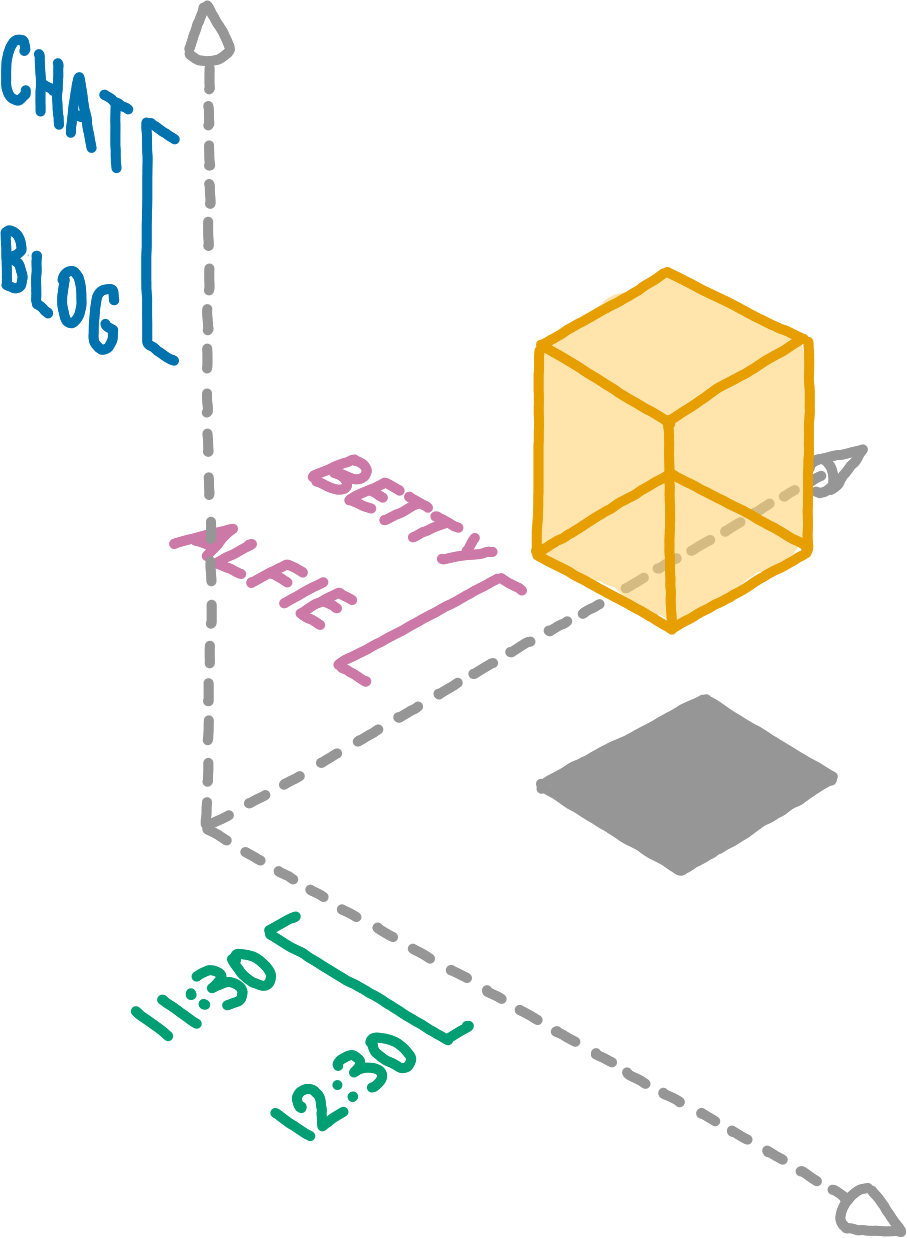A 3dRange composed of a SubspaceRange, PathRange, and TimeRange.When we combine ranges of all three dimensions, we can delimit boxes in Willow space.
}A 3dRange includes every Entry whose subspace_id, path, and timestamp are all included their respective range.
We define default_3d_range(default_subspace) to denote the 3dRange with the following members:
Areas
3dRanges provide a natural way of grouping Entries, but they have certain drawbacks around encrypted data in Willow: when encrypting Paths, for example, the lexicographic ordering of the encrypted Paths is inconsistent with the ordering of the unencrypted Paths. Similarly, SubspaceRanges do not preserve their meaning under encryption either. Hence, user-specified 3dRanges are close to useless when dealing with encrypted data.
Fortunately, there do exist encryption techniques that preserve some weaker properties than arbitrary orderings.See invalid-reference for information on encrypting Willow. Without going into the cryptographic details, we now define an alternative to 3dRanges that can be used even when encrypting Paths and SubspaceIds.
Every Area can be expressed as a 3dRange, but not the other way around. Areas always denote boxes in Willow space, but some boxes do not correspond to any Area.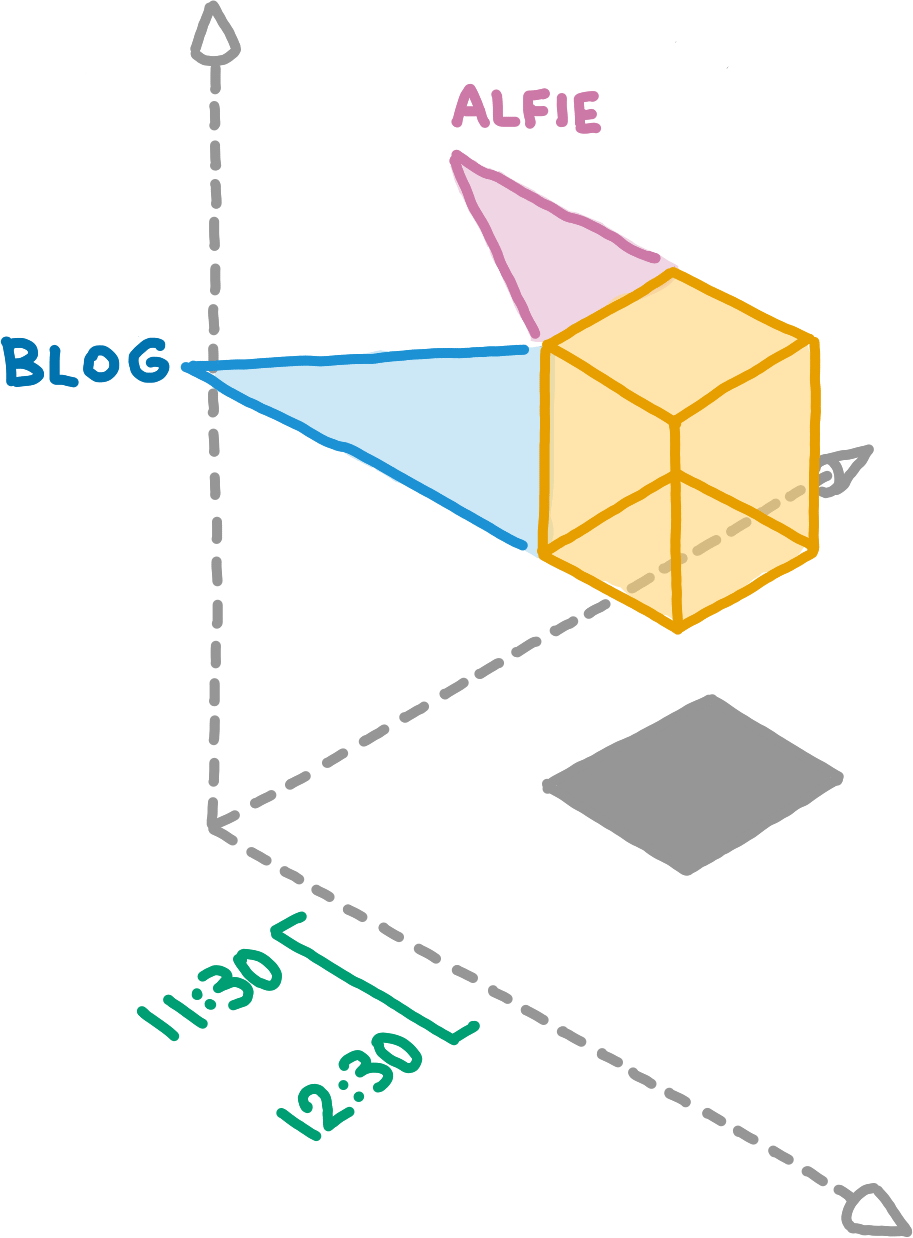
This diagram attempts to show the key difference between a 3dRange and an Area, namely that its dimensions are derived from its subspace_id and its path.
A grouping of Entries. To be included in this Area, an Entry’s subspace_id must be equal to the subspace_id, unless it is any.}An Area a includes an Entry e if
a.subspace_id == any or a.subspace_id == e.subspace_id,- a.path is a prefix of e.path, and
- times.path includes e.timestamp.
An Area is empty if it includes no Entries. This is the case if and only if its times is empty.
An Area includes another Area if the first Area includes all Entries that the second Area includes. In particular, every Area includes itself.
The full area is the Area whose subspace_id is any, whose path is the empty Path, and whose times is the open TimeRange with start It includes all Entries.
The subspace area of the SubspaceId sub is the Area whose subspace_id is sub, whose path is the empty Path, and whose times is the open TimeRange with start It includes exactly the Entries with subspace_id sub.
If two Areas overlap, the overlap is again an Area. Let a1 and a2 be Areas. If there exists at least one Entry included in both a1, and a2, then we define the (nonempty) intersection of a1, and a2 as the Area whose
- subspace_id is a1.subspace_id if a1.subspace_id is not any, or a2.subspace_id otherwise, whose
- path is the longer of a1.path andOne is a prefix of the other, otherwise the intersection would be empty. a2.path, and whose
- times is the intersection of a1.times and a2.times.
Areas of Interest
Occasionally, we wish to group Entries based on the contents of some store. For example, a space-constrained peer might ask for the 100 newest Entries of some store when synchronising data.
We serve these use cases by combining an Area with limits to restrict the contents to the Entries with the greatest entry_timestamp.
The total entry_payload_length of all included Entries is at most max_size, unless max_size is zero.}An AreaOfInterest aoi includes an Entry e from a store s if
- aoi.area includes e,
- aoi.max_count is zero, or e is among the aoi.max_count newest Entries of s, and
- aoi.max_size is zero, or the sum of the entry_payload_length of e and all newer Entries in s is less than or equal to aoi.max_size.
Let aoi1 and aoi2 be AreasOfInterest. If there exists at least one Entry included in both aoi1.area and aoi2.area, then we define the (nonempty) intersection of aoi1, and aoi2 as the AreaOfInterest whose